A/B测试系列文章之A/B测试背后的科学原理

以后文章更新会先在微信公众号（公众号名：输出ING），欢迎大家来关注。

前面Jeff 专门讨论了A/B测试里两个常见统计问题——样本量计算和显著性计算，这篇我们来看下A/B 测试背后的科学原理。

因果推断

因果推断是什么？维基百科是这么介绍的：

Causal inference is the process of drawing a conclusion about a causal connection based on the conditions of the occurrence of an effect.

https://en.wikipedia.org/wiki/Causal_inference

用中文翻译就是：因果推断是指在一种现象已经发生的情况下推出因果关系结论的过程。比如说全球气候变暖，需要分析是什么因素导致的，各个因素对全球气候变暖影响有多大。

因果推断要做的是识别因果关系，量化因果作用。而这也是A/B 测试要做的事情，即根据实验结果判断新版相比原来版本有无显著提升，如果有，提升了多少。随机化试验是因果推断的黄金法则，在心理学等领域有着广泛的应用，而A/B 测试恰好是随机化试验在互联网的应用。

根据因果推断随机化试验相关知识，如果实验组和对照组的实验结果指标有显著差异，那差异原因就来自于A、B两个不同版本（比如不同的文案、不同的按钮颜色、不同的推荐策略等）而非其他，且A、B两版本差异的大小就是新的实验方案对结果指标带来的作用大小。

假设检验

A/B 试验最终要观察的一般是A、B两组实验结果指标的差异，比如说人均时长、留存率、激活转化率，这些都可以看做A、B两组均值的比较。而A、B两组均值比较可以转化为对于假设H0：A、B两组实验结果指标不存在显著差异的反证，这就是假设检验。即先有一个假设，然后根据抽样统计到的数据去检验假设能否被推翻，若能被推翻，则认为假设H0不成立。

根据假设检验的思想，就可以在实验前计算实验需要多少样本量，在实验后计算实验结果显著性。

中心极限定理

常用的假设检验有不少，如t检验、Z检验、F检验、卡方检验等。那么之前的计算为何用的Z检验呢？这主要是基于中心极限定理。中心极限定理在教材上的表述如下：

这个定理看似有点反直觉，但如果真的理解其含义会发现也很自然。以下是统计学课本上常用的中心极限定理的图例说明：

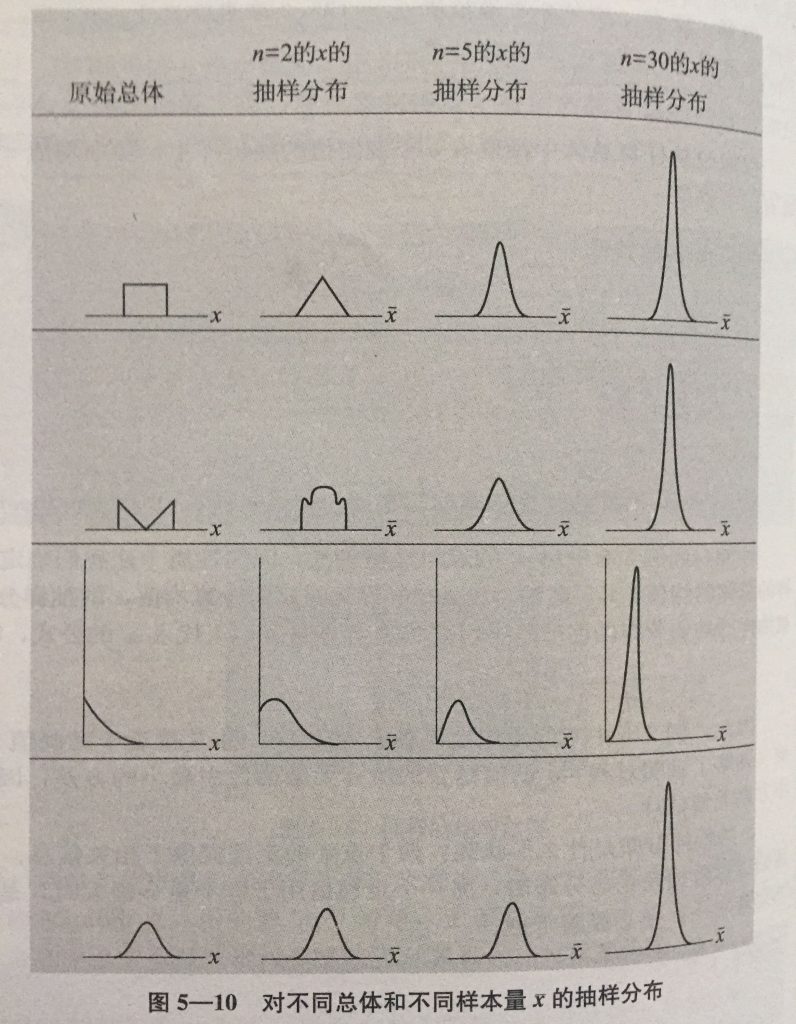
根据这个定理，不管实验关注的结果指标自身分布如何，比如点赞次数、评论次数、分享次数，这些肯定不是呈正态分布。但是只要实验随机地选取用户且用户量足够大，那么每次抽样的均值作为一个样本点形成的分布会呈现正态分布。且抽样分布的均值近似为总体均值，抽样分布的标准差为总体方差的1/sqrt(n)。

实际的社会生活中，要统计总体的一些数值的成本可能非常高，基本不可行，比如统计特朗普在美国民众中的支持率，但可以通过随机抽样得到的数据来进行估计。随着抽样选取的样本数量越大，抽样得到的数值跟真实值就越接近。

正因为A/B 测试是随机分流，且实验样本量远远大于统计学上所说的大样本量（样本量n>30），这就满足了中心极限定理，而大样本量条件下总体方差可近似用样本方差来近似，因此可以使用两独立样本Z检验的方法。

卡方检验与Z检验

前面有提到，对于A/B 测试中样本量计算和显著性计算都可以采用Z检验相关的公式来完成，但你可能注意到显著性计算文章中给出的在线工具使用的是卡方检验而非Z检验。这是为何呢？

这是因为，对于比例类指标的A/B 实验，其显著性检验可以等价为2x2双向列联表独立性检验。即一个维度为实验版本（分别为A、B），另一个为维度为是否转化（分别为成功转化、未成功转化）。可以证明，在这种特殊情况下，两种检验方式在数学上是等价的。因此计算比例类指标显著性时也可以使用卡方检验的函数，比如用R中的chisq.test和prop.test可以得到一样的p值。

总结一下：因为A/B 随机分流，所以A、B的结果指标有显著差异就是A、B两种不同的方案带来的。A、B结果指标的比较可以先假设A、B不存在显著差异，从而在实验前计算实验所需样本量，在实验后计算实验结果显著性。A/B 测试由于是随机分流且样本量也足够大，因而可以用正态分布Z检验来比较A、B两组是否有显著差异。特别地，对于两样本比例指标的显著性检验，2x2双向列联表的卡方检验等价于Z检验。